

The goal of forrel is to provide forensic pedigree computations and relatedness inference from genetic marker data. The forrel package is part of the pedsuite, a collection of R packages for pedigree analysis.
The most important analyses currently supported by forrel are:
quickLR()kinshipLR()ibdEstimate()ibdBootstrap()checkPairwise()markerSim()profileSim()markerSimParametric()profileSimParametric()LRpower()exclusionPower()missingPersonPlot()missingPersonEP()missingPersonIP()MPPsims()powerPlot()rankProfiles()To get the current official version of forrel, install from CRAN as follows:
install.packages("forrel")Alternatively, you can obtain the latest development version from GitHub:
# install.packages("remotes") # if needed
remotes::install_github("magnusdv/forrel")In this short introduction, we first demonstrate simulation of marker data for a pair of siblings. Then - pretending the relationship is unknown to us - we estimate the relatedness between the brothers using the simulated data. If all goes well, the estimate should be close to the expected value for siblings.
library(forrel)
#> Loading required package: pedtoolsCreate the pedigree
We start by creating and plotting a pedigree with two brothers, named
bro1 and bro2.
x = nuclearPed(children = c("bro1", "bro2"))
plot(x)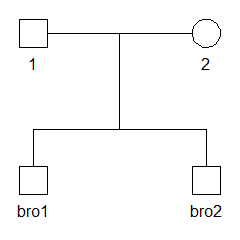
Marker simulation
Now let us simulate the genotypes of 100 independent SNPs for all four family members. Each SNP has alleles 1 and 2, with equal frequencies by default. This is an example of unconditional simulation, since we don’t give any genotypes to condition on.
x = markerSim(x, N = 100, alleles = 1:2, seed = 1234)
#> Unconditional simulation of 100 autosomal markers.
#> Individuals: 1, 2, bro1, bro2
#> Allele frequencies:
#> 1 2
#> 0.5 0.5
#> Mutation model: No
#>
#> Simulation finished.
#> Calls to `likelihood()`: 0.
#> Total time used: 0.07 seconds.Note 1: The seed argument is passed onto the random
number generator. If you use the same seed, you should get exactly the
same results.
Note 2: To suppress the informative messages printed during simulation,
add verbose = FALSE to the function call.
The pedigree x now has 100 markers attached to it. The
genotypes of the first few markers are shown when printing
x to the screen:
x
#> id fid mid sex <1> <2> <3> <4> <5>
#> 1 * * 1 1/2 1/2 1/1 2/2 2/2
#> 2 * * 2 1/1 1/2 1/1 1/1 2/2
#> bro1 1 2 1 1/1 1/2 1/1 1/2 2/2
#> bro2 1 2 1 1/1 1/2 1/1 1/2 2/2
#> Only 5 (out of 100) markers are shown.Conditional simulation
Suppose one of the brothers is homozygous 1/1 and that we want to
simulate genotypes for the other brother. This is achieved with the
following code, where after first attaching a marker to the pedigree,
specifying the known genotype, we condition on it by referencing it in
markerSim().
y = nuclearPed(children = c("bro1", "bro2")) |>
addMarker(bro1 = "1/1", alleles = 1:2, name = "snp1") |>
markerSim(N = 100, ids = "bro2", partialmarker = "snp1",
seed = 321, verbose = FALSE)
y
#> id fid mid sex <1> <2> <3> <4> <5>
#> 1 * * 1 -/- -/- -/- -/- -/-
#> 2 * * 2 -/- -/- -/- -/- -/-
#> bro1 1 2 1 1/1 1/1 1/1 1/1 1/1
#> bro2 1 2 1 2/2 1/2 1/1 1/1 1/1
#> Only 5 (out of 100) markers are shown.Note that the previous code also demonstrates how
pedsuite is well adapted to the R pipe
|>.
Estimation of IBD coefficients
The ibdEstimate() function estimates the coefficients of
identity-by-descent (IBD) between pairs of individuals, from
the available marker data. Let us try with the simulated genotypes we
just generated:
k = ibdEstimate(y, ids = c("bro1", "bro2"))
#> Estimating 'kappa' coefficients
#> Initial search value: (0.333, 0.333, 0.333)
#> Pairs of individuals: 1
#> bro1 vs. bro2: estimate = (0.28, 0.54, 0.18), iterations = 10
#> Total time: 0.00512 secs
k
#> id1 id2 N k0 k1 k2
#> 1 bro1 bro2 100 0.28001 0.53998 0.18001To get a visual sense of the estimate, it is instructive to plot it in the IBD triangle:
showInTriangle(k, labels = TRUE)
Reassuringly, the estimate is close to the theoretical expectation
for non-inbred full siblings, \((\kappa_0,
\kappa_1, \kappa_2) = (0.25, 0.5, 0.25)\), corresponding to the
point marked S in the triangle.